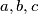
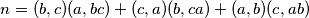
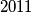
We call a positive integer amazing if there exist positive integers such that the equality holds. Prove that there exist consecutive positive integers which are amazing.
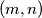
Note. By we denote the greatest common divisor of positive integers and .
%V0
We call a positive integer $n$ amazing if there exist positive integers $a, b, c$ such that the equality $$n = (b, c)(a, bc) + (c, a)(b, ca) + (a, b)(c, ab)$$ holds. Prove that there exist $2011$ consecutive positive integers which are amazing.
Note. By $(m, n)$ we denote the greatest common divisor of positive integers $m$ and $n$.
Izvor: Srednjoeuropska matematička olimpijada 2011, ekipno natjecanje, problem 8
Školjka 
amazing if there exist positive integers 
such that the equality 
holds. Prove that there exist 
consecutive positive integers which are amazing.
we denote the greatest common divisor of positive integers 
and