U trokutu

je
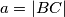
,
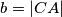
,
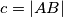
,
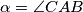
,
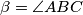
,
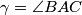
.

Ako je
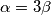
, dokažite da je
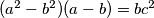
.

Vrijedi li obrat? Obrazložite.
%V0
U trokutu $ABC$ je $a = |BC|$, $b = |CA|$, $c = |AB|$, $\alpha = \angle CAB$, $\beta = \angle ABC$, $\gamma = \angle BAC$.
$a)$ Ako je $\alpha = 3\beta$, dokažite da je $(a^2 - b^2)(a - b) = bc^2$.
$b)$ Vrijedi li obrat? Obrazložite.