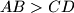
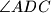
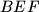
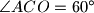
In a given trapezium with parallel to and , the line bisects the angle . The line through parallel to meets the segments and in and , respectively. Let be the circumcenter of the triangle . Suppose that . Prove the equality
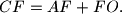
%V0
In a given trapezium $ABCD$ with $AB$ parallel to $CD$ and $AB > CD$, the line $BD$ bisects the angle $\angle ADC$. The line through $C$ parallel to $AD$ meets the segments $BD$ and $AB$ in $E$ and $F$, respectively. Let $O$ be the circumcenter of the triangle $BEF$. Suppose that $\angle ACO = 60^{\circ}$. Prove the equality
$$CF = AF + FO .$$
Izvor: Srednjoeuropska matematička olimpijada 2012, pojedinačno natjecanje, problem 3
Školjka 
with 
parallel to 
and 
, the line 
bisects the angle 
. The line through 
parallel to 
meets the segments 
and 
, respectively. Let 
be the circumcenter of the triangle 
. Suppose that 
. Prove the equality