MEMO 2012 pojedinačno problem 4
Dodao/la:
arhiva23. lipnja 2013. The sequence
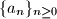
is defined by
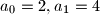
and
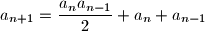
for all positive integers

. Determine all prime numbers

for which there exists a positive integer

such that

divides the number
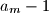
.
%V0
The sequence $\{ a_n \} _ { n \ge 0 }$ is defined by $a_0 = 2 , a_1 = 4$ and
$$a_{n+1} = \frac{a_n a_{n-1}}{2} + a_n + a_{n-1}$$
for all positive integers $n$. Determine all prime numbers $p$ for which there exists a positive integer $m$ such that $p$ divides the number $a_m - 1$.
Izvor: Srednjoeuropska matematička olimpijada 2012, pojedinačno natjecanje, problem 4