MEMO 2012 ekipno problem 4
Dodao/la:
arhiva23. lipnja 2013. Let
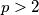
be a prime number. For any permutation

of the set
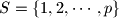
, let
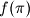
denote the number of multiples of

among the following

numbers:
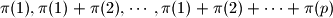
Determine the average value of
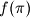
taken over all permutations
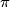
of

.
%V0
Let $p>2$ be a prime number. For any permutation $\pi = ( \pi(1) , \pi(2) , \cdots , \pi(p) )$ of the set $S = \{ 1, 2, \cdots , p \}$, let $f( \pi )$ denote the number of multiples of $p$ among the following $p$ numbers:
$$\pi(1) , \pi(1) + \pi(2) , \cdots , \pi(1) + \pi(2) + \cdots + \pi(p)$$
Determine the average value of $f( \pi)$ taken over all permutations $\pi$ of $S$.
Izvor: Srednjoeuropska matematička olimpijada 2012, ekipno natjecanje, problem 4