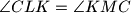
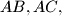
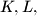
Let be the midpoint of the side of a given triangle . Let and be points on the sides and , respectively, such that . Prove that the perpendiculars to the sides and passing through and , respectively, are concurrent.
%V0
Let $K$ be the midpoint of the side $AB$ of a given triangle $ABC$. Let $L$ and $M$ be points on the sides $AC$ and $BC$, respectively, such that $\angle CLK = \angle KMC$. Prove that the perpendiculars to the sides $AB, AC,$ and $BC$ passing through $K,L,$ and $M$, respectively, are concurrent.
Izvor: Srednjoeuropska matematička olimpijada 2012, ekipno natjecanje, problem 5
Školjka 
be the midpoint of the side 
of a given triangle 
. Let 
and 
be points on the sides 
and 
, respectively, such that 
. Prove that the perpendiculars to the sides 
and 
and