MEMO 2012 ekipno problem 6
Kvaliteta:
Avg: 3,5Težina:
Avg: 6,0 Let  be a convex quadrilateral with no pair of parallel sides, such that
be a convex quadrilateral with no pair of parallel sides, such that 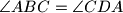 . Assume that the intersections of the pairs of neighbouring angle bisectors of
. Assume that the intersections of the pairs of neighbouring angle bisectors of  form a convex quadrilateral
form a convex quadrilateral 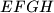 . Let
. Let  be the intersection of the diagonals of
be the intersection of the diagonals of 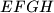 . Prove that the lines
. Prove that the lines  and
and  intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle 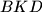 .
.
 be a convex quadrilateral with no pair of parallel sides, such that
be a convex quadrilateral with no pair of parallel sides, such that 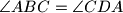 . Assume that the intersections of the pairs of neighbouring angle bisectors of
. Assume that the intersections of the pairs of neighbouring angle bisectors of  form a convex quadrilateral
form a convex quadrilateral 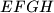 . Let
. Let  be the intersection of the diagonals of
be the intersection of the diagonals of 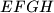 . Prove that the lines
. Prove that the lines  and
and  intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle 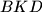 .
. Izvor: Srednjoeuropska matematička olimpijada 2012, ekipno natjecanje, problem 6
 Školjka
Školjka 
