Županijsko natjecanje 2013 SŠ3 1
Dodao/la:
arhiva12. srpnja 2013. Dane su tri kolinearne točke

,

i

, takve da je

između

i

, te kružnica

čiji je promjer

. Neka je

bilo koja točka na kružnici

, različita od

i

. Dokaži da je vrijednost izraza
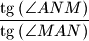
konstantna, tj. da ne ovisi o odabiru točke

.
%V0
Dane su tri kolinearne točke $A$, $B$ i $M$, takve da je $M$ između $A$ i $B$, te kružnica $k$ čiji je promjer $\overline{AB}$. Neka je $N$ bilo koja točka na kružnici $k$, različita od $A$ i $B$. Dokaži da je vrijednost izraza $$\displaystyle \frac{\tg{\left(\angle ANM\right)}}{\tg{\left(\angle MAN\right)}}$$ konstantna, tj. da ne ovisi o odabiru točke $N$.
Izvor: Županijsko natjecanje iz matematike 2013