Neka je točka

središte opisane kružnice trokuta

s kutovima
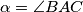
i
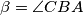
. Neka pravac
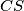
siječe pravac

u točki

koja se nalazi između točaka

i

. Dokaži da vrijedi
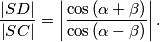
%V0
Neka je točka $S$ središte opisane kružnice trokuta $ABC$ s kutovima $\alpha=\angle{BAC}$ i $\beta = \angle{CBA}$. Neka pravac $CS$ siječe pravac $AB$ u točki $D$ koja se nalazi između točaka $A$ i $B$. Dokaži da vrijedi $$ \frac{\left\vert SD \right\vert}{\left\vert SC \right\vert} = \left\vert \frac{\cos\left(\alpha + \beta\right)}{\cos\left(\alpha-\beta\right)}\right\vert \text{.} $$