Dan je pravokutan trokut

s pravim kutom pri vrhu

, u kojem je

polovište katete

. Dokaži da je
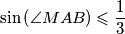
. Kada se postiže jednakost?
%V0
Dan je pravokutan trokut $ABC$ s pravim kutom pri vrhu $C$, u kojem je $M$ polovište katete $\overline{BC}$. Dokaži da je $\displaystyle \sin\left(\angle{MAB}\right) \leqslant \frac 13$. Kada se postiže jednakost?