Školjka

%V0 U šiljastokutnom trokutu $ABC$ udaljenosti od vrha $A$ do središta opisane kružnice i ortocentra su jednake. Izračunati kut $\alpha = \angle BAC$.

%V0 Duljine stranica trokuta su tri uzastopna prirodna broja, a jedan od kutova trokuta je dvaput veci od jednog od preostalih dvaju kutova. Odredi duljine stranica trokuta.

%V0 Neka je $ABC$ trokut u kojem vrijedi $\left\vert AC \right\vert > \left\vert BC \right\vert$. Izrazi površinu trokuta određenog stranicom $\overline{AB}$, simetralom stranice $\overline{AB}$ i simetralom kuta $\angle{ACB}$ pomoću duljina stranica trokuta $ABC$.

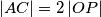
%V0 Neka je točka $S$ središte opisane kružnice trokuta $ABC$ s kutovima $\alpha=\angle{BAC}$ i $\beta = \angle{CBA}$. Neka pravac $CS$ siječe pravac $AB$ u točki $D$ koja se nalazi između točaka $A$ i $B$. Dokaži da vrijedi $$ \frac{\left\vert SD \right\vert}{\left\vert SC \right\vert} = \left\vert \frac{\cos\left(\alpha + \beta\right)}{\cos\left(\alpha-\beta\right)}\right\vert \text{.} $$

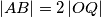
%V0 Neka je točka $N$ nožište visine iz vrha $A$ šiljastokutnog trokuta $ABC$, točke $P$ i $Q$ redom nožišta okomica iz točke $N$ na stranice $\overline{AB}$ i $\overline{AC}$, a točka $O$ središte opisane kružnice danog trokuta. Ako vrijedi $\left\vert AC \right\vert = 2\left\vert OP \right\vert$, dokaži da vrijedi $\left\vert AB \right\vert = 2\left\vert OQ \right\vert$.

%V0 Dan je pravokutan trokut $ABC$ s pravim kutom pri vrhu $C$, u kojem je $M$ polovište katete $\overline{BC}$. Dokaži da je $\displaystyle \sin\left(\angle{MAB}\right) \leqslant \frac 13$. Kada se postiže jednakost?