Neka je

prirodan broj koji se može prikazivati kao suma kvadrata dvaju prirodnih brojeva na dva različita načina:
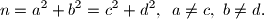
Dokažite da je

složen broj.
%V0
Neka je $n$ prirodan broj koji se može prikazivati kao suma kvadrata dvaju prirodnih brojeva na dva različita načina:
$$n=a^2+b^2=c^2+d^2, \,\,\, a \neq c, \,\, b \neq d.$$
Dokažite da je $n$ složen broj.