Slični zadaci
Na slici su unutar kružnice sa središtem  i polumjerom
i polumjerom  nacrtani lukovi još šest kružnica istog polumjera. U području između dvije susjedne "latice" upisan je niz kružnica s polumjerima
nacrtani lukovi još šest kružnica istog polumjera. U području između dvije susjedne "latice" upisan je niz kružnica s polumjerima 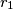 ,
, 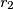 ,
, 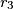 , ..., koje se s početnom kružnicom i susjednim kružnicama u nizu dodiruju redom u točkama
, ..., koje se s početnom kružnicom i susjednim kružnicama u nizu dodiruju redom u točkama 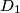 ,
, 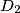 ,
, 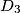 , ... . Za svaki
, ... . Za svaki  izračunajte polumjer
izračunajte polumjer 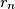 i duljinu
i duljinu 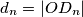 .
.
{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
 i polumjerom
i polumjerom  nacrtani lukovi još šest kružnica istog polumjera. U području između dvije susjedne "latice" upisan je niz kružnica s polumjerima
nacrtani lukovi još šest kružnica istog polumjera. U području između dvije susjedne "latice" upisan je niz kružnica s polumjerima 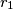 ,
, 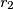 ,
, 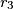 , ..., koje se s početnom kružnicom i susjednim kružnicama u nizu dodiruju redom u točkama
, ..., koje se s početnom kružnicom i susjednim kružnicama u nizu dodiruju redom u točkama 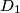 ,
, 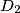 ,
, 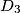 , ... . Za svaki
, ... . Za svaki  izračunajte polumjer
izračunajte polumjer 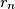 i duljinu
i duljinu 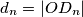 .
.{{ Greška pri preuzimanju img datoteke. (Nevaljan broj?) }}
 Školjka
Školjka 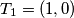 ,
, 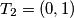 ,
, 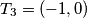 ,
, 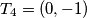 . za svaki
. za svaki  neka je
neka je 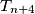 poloviste duzine
poloviste duzine 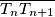 . uz pretpostavku da niz tocaka
. uz pretpostavku da niz tocaka 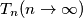 ima granicnu tocku, nadite koordinate te tocke.
ima granicnu tocku, nadite koordinate te tocke.  tocka na simetrali kuta
tocka na simetrali kuta  trokuta
trokuta  , a
, a  i
i  redom tocke na stranicama
redom tocke na stranicama  i
i  , takve da je
, takve da je 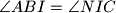 i
i 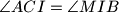 . dokazite da je
. dokazite da je  i odgovarajucim kutevima
i odgovarajucim kutevima 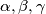 postoje tocke
postoje tocke  i
i  takve da vrijedi
takve da vrijedi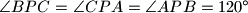 ,
,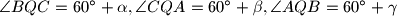 .
.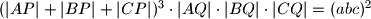
 konveksni cetverokut i neka su
konveksni cetverokut i neka su  i
i  takve da je
takve da je 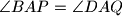 . dokazite da trokuti
. dokazite da trokuti 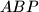 i
i 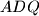 imaju jednake povrsine ako i samo ako je spojnica njihovih ortocentara okomita na pravac
imaju jednake povrsine ako i samo ako je spojnica njihovih ortocentara okomita na pravac  .
. 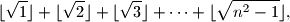 gdje je
gdje je 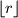 najveći cijeli broj koji nije veći od
najveći cijeli broj koji nije veći od  .
. 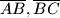 trokuta
trokuta 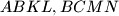 (koji s trokutom imaju samo zajednicku stranicu).
(koji s trokutom imaju samo zajednicku stranicu). tocka takva da je
tocka takva da je  i
i 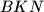 sukladni.
sukladni.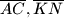 i sredista kvadrata
i sredista kvadrata