MEMO 2013 pojedinačno problem 1
Dodao/la:
arhiva24. rujna 2014. Neka su

pozitivni realni brojevi takvi da vrijedi
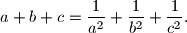
Dokaži
![2(a + b + c) \geq \sqrt[3]{7a^2b + 1} + \sqrt[3]{7b^2c + 1} + \sqrt[3]{7c^2a + 1} \text{.}](/media/m/b/d/5/bd5f82834e8a41edd87111ad765bc5c5.png)
Nađi sve trojke
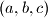
za koje vrijedi jednakost.
%V0
Neka su $a, b, c$ pozitivni realni brojevi takvi da vrijedi $$
a + b + c = \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2} \text{.}
$$ Dokaži $$
2(a + b + c) \geq \sqrt[3]{7a^2b + 1} + \sqrt[3]{7b^2c + 1} + \sqrt[3]{7c^2a + 1} \text{.}
$$ Nađi sve trojke $(a, b, c)$ za koje vrijedi jednakost.
Izvor: Srednjoeuropska matematička olimpijada 2013, pojedinačno natjecanje, problem 1