MEMO 2013 pojedinačno problem 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Neka je  prirodni broj. Na ploču koja se sastoji od
prirodni broj. Na ploču koja se sastoji od 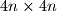 kvadrata postavljeno je točno
kvadrata postavljeno je točno 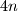 žetona tako da se u svakom retku i svakom stupcu nalazi točno jedan žeton. U jednom koraku, jedan žeton pomičemo horizontalno ili vertikalno na susjedni kvadrat. Više žetona se u nekom trenutku može nalaziti na istom kvadratu. Žetone trebamo pomaknuti tako da zauzimaju sve kvadrate jedne od dviju dijagonala.
žetona tako da se u svakom retku i svakom stupcu nalazi točno jedan žeton. U jednom koraku, jedan žeton pomičemo horizontalno ili vertikalno na susjedni kvadrat. Više žetona se u nekom trenutku može nalaziti na istom kvadratu. Žetone trebamo pomaknuti tako da zauzimaju sve kvadrate jedne od dviju dijagonala.
Odredi najmanji broj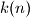 takav da to možemo postići u najviše
takav da to možemo postići u najviše 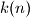 koraka za bilo koji početni raspored.
koraka za bilo koji početni raspored.
 prirodni broj. Na ploču koja se sastoji od
prirodni broj. Na ploču koja se sastoji od 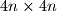 kvadrata postavljeno je točno
kvadrata postavljeno je točno 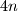 žetona tako da se u svakom retku i svakom stupcu nalazi točno jedan žeton. U jednom koraku, jedan žeton pomičemo horizontalno ili vertikalno na susjedni kvadrat. Više žetona se u nekom trenutku može nalaziti na istom kvadratu. Žetone trebamo pomaknuti tako da zauzimaju sve kvadrate jedne od dviju dijagonala.
žetona tako da se u svakom retku i svakom stupcu nalazi točno jedan žeton. U jednom koraku, jedan žeton pomičemo horizontalno ili vertikalno na susjedni kvadrat. Više žetona se u nekom trenutku može nalaziti na istom kvadratu. Žetone trebamo pomaknuti tako da zauzimaju sve kvadrate jedne od dviju dijagonala.Odredi najmanji broj
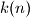 takav da to možemo postići u najviše
takav da to možemo postići u najviše 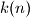 koraka za bilo koji početni raspored.
koraka za bilo koji početni raspored. Izvor: Srednjoeuropska matematička olimpijada 2013, pojedinačno natjecanje, problem 2
 Školjka
Školjka 
