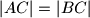
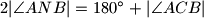
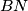
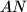
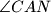
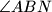
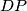
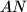
Neka je jednakokračni trokut takav da je . Neka je točka unutar tog trokuta takva da je . Neka je sjecište pravca i pravca paralelnog pravcu koji prolazi točkom . Neka je sjecište simetrale i simetrale . Dokaži da su pravci i međusobno okomiti.
%V0
Neka je $ABC$ jednakokračni trokut takav da je $|AC| = |BC|$. Neka je $N$ točka unutar tog trokuta takva da je $2|\angle ANB| = 180^\circ + |\angle ACB|$. Neka je $D$ sjecište pravca $BN$ i pravca paralelnog pravcu $AN$ koji prolazi točkom $C$. Neka je $P$ sjecište simetrale $\angle CAN$ i simetrale $\angle ABN$.
Dokaži da su pravci $DP$ i $AN$ međusobno okomiti.
Izvor: Srednjoeuropska matematička olimpijada 2013, pojedinačno natjecanje, problem 3
Školjka 
jednakokračni trokut takav da je 
. Neka je 
točka unutar tog trokuta takva da je 
. Neka je 
sjecište pravca 
i pravca paralelnog pravcu 
koji prolazi točkom 
. Neka je 
sjecište simetrale 
i simetrale 
.
i