MEMO 2013 ekipno problem 5
Dodao/la:
arhiva24. rujna 2014. Neka je

šiljastokutni trokut. Konstruirajte trokut
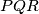
takav da je
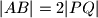
,
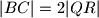
,
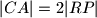
, a pravci

,
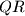
i
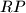
prolaze točkama

,

i

, redom. (Točke
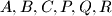
su međusobno različite.)
%V0
Neka je $ABC$ šiljastokutni trokut. Konstruirajte trokut $PQR$ takav da je $|AB| = 2|PQ|$, $|BC| = 2|QR|$, $|CA| = 2|RP|$, a pravci $PQ$, $QR$ i $RP$ prolaze točkama $A$, $B$ i $C$, redom. (Točke $A, B, C, P, Q, R$ su međusobno različite.)
Izvor: Srednjoeuropska matematička olimpijada 2013, ekipno natjecanje, problem 5