MEMO 2014 pojedinačno problem 3
Dodao/la:
arhiva24. rujna 2014. Let

be a triangle with
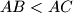
and incentre

. Let

be the point on the side

such that

. Let

be the point on the line
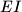
such that
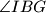
=
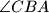
and such that

and

lie on opposite sides of

.
Prove that the line
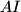
, the perpendicular to
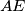
at

, and the bisector of the angle
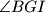
are concurrent.
%V0
Let $ABC$ be a triangle with $AB < AC$ and incentre $I$. Let $E$ be the point on the side $AC$ such that $AE = AB$. Let $G$ be the point on the line $EI$ such that $\angle IBG$ = $\angle CBA$ and such that $E$ and $G$ lie on opposite sides of $I$.
Prove that the line $AI$, the perpendicular to $AE$ at $E$, and the bisector of the angle $\angle BGI$ are concurrent.
Izvor: Srednjoeuropska matematička olimpijada 2014, pojedinačno natjecanje, problem 3