MEMO 2014 pojedinačno problem 4
Kvaliteta:
Avg: 3,0Težina:
Avg: 5,0 For integers 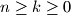 we define the bibinomial coefficient
we define the bibinomial coefficient 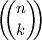 by
by 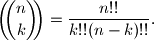 Determine all pairs
Determine all pairs 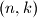 of integers with
of integers with 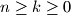 such that the corresponding bibinomial coefficient is an integer.
such that the corresponding bibinomial coefficient is an integer.
Remark. The double factorial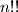 is defined to be the product of all even positive integers up to
is defined to be the product of all even positive integers up to  if
if  is even and the product of all odd positive integers up to
is even and the product of all odd positive integers up to  if
if  is odd. So e.g.
is odd. So e.g. 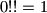 ,
, 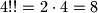 , and
, and 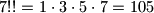 .
.
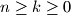 we define the bibinomial coefficient
we define the bibinomial coefficient 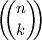 by
by 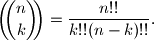 Determine all pairs
Determine all pairs 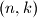 of integers with
of integers with 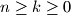 such that the corresponding bibinomial coefficient is an integer.
such that the corresponding bibinomial coefficient is an integer.Remark. The double factorial
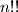 is defined to be the product of all even positive integers up to
is defined to be the product of all even positive integers up to  if
if  is even and the product of all odd positive integers up to
is even and the product of all odd positive integers up to  if
if  is odd. So e.g.
is odd. So e.g. 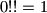 ,
, 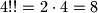 , and
, and 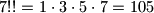 .
. Izvor: Srednjoeuropska matematička olimpijada 2014, pojedinačno natjecanje, problem 4
 Školjka
Školjka 
