MEMO 2014 ekipno problem 1
Dodao/la:
arhiva24. rujna 2014. Determine the lowest possible value of the expression
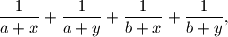
where

,

,

, and

are positive real numbers satisfying the inequalities
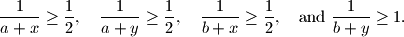
%V0
Determine the lowest possible value of the expression $$
\frac{1}{a + x} + \frac{1}{a + y} + \frac{1}{b + x} + \frac{1}{b + y} \text{,}
$$ where $a$, $b$, $x$, and $y$ are positive real numbers satisfying the inequalities $$
\frac{1}{a + x} \geq \frac12, \quad
\frac{1}{a + y} \geq \frac12, \quad
\frac{1}{b + x} \geq \frac12, \quad \text{and}
\ \frac{1}{b + y} \geq 1 \text{.}
$$
Izvor: Srednjoeuropska matematička olimpijada 2014, ekipno natjecanje, problem 1