Dana je točka
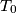
na paraboli
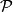
s jednadžbom
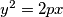
i točka
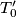
takva da je polovište dužine
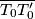
na osi parabole
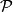
. Za varijabilnu točku

na
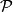
, različitu od
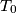
i njoj simetrične točke s obzirom na os parabole, okomica iz točke
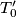
na pravac
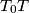
siječe paralelu s osi parabole kroz točku

u točki
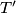
. Što opisuje točka
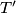
?
%V0
Dana je točka $T_0$ na paraboli $\mathcal{P}$ s jednadžbom $y^2 = 2px$ i točka $T_0^\prime$ takva da je polovište dužine $\overline{T_0 T_0^\prime}$ na osi parabole $\mathcal{P}$. Za varijabilnu točku $T$ na $\mathcal{P}$, različitu od $T_0$ i njoj simetrične točke s obzirom na os parabole, okomica iz točke $T_0^\prime$ na pravac $T_0 T$ siječe paralelu s osi parabole kroz točku $T$ u točki $T^\prime$. Što opisuje točka $T^\prime$?