MEMO 2014 ekipno problem 5
Dodao/la:
arhiva24. rujna 2014. Let

be a triangle with
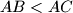
. Its incircle with centre

touches the sides

,

, and

in the points

,

, and

respectively. The angle bisector
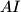
intersects the lines
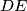
and
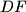
in the points

and
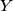
respectively. Let
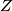
be the foot of the altitude through

with respect to

.
Prove that

is the incentre of the triangle
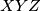
.
%V0
Let $ABC$ be a triangle with $AB < AC$. Its incircle with centre $I$ touches the sides $BC$, $CA$, and $AB$ in the points $D$, $E$, and $F$ respectively. The angle bisector $AI$ intersects the lines $DE$ and $DF$ in the points $X$ and $Y$ respectively. Let $Z$ be the foot of the altitude through $A$ with respect to $BC$.
Prove that $D$ is the incentre of the triangle $XYZ$.
Izvor: Srednjoeuropska matematička olimpijada 2014, ekipno natjecanje, problem 5