Državno natjecanje 2000 SŠ1 3
Dodao/la:
arhiva1. travnja 2012. Neka je
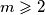
prirodan broj. Koliko rješenja u skupu prirodnih brojeva ima jednadžba
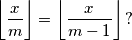
(
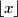
je oznaka za najveći cijeli broj koji nije veći od

.)
%V0
Neka je $m \geqslant 2$ prirodan broj. Koliko rješenja u skupu prirodnih brojeva ima jednadžba $$\left\lfloor{\vphantom{\frac{x}{m-1}}\frac{x}{m}}\right\rfloor = \left\lfloor{\frac{x}{m-1}}\right\rfloor \text{?}$$
($\left\lfloor x \right\rfloor$ je oznaka za najveći cijeli broj koji nije veći od $x$.)
Izvor: Državno natjecanje iz matematike 2000