Županijsko natjecanje iz matematike 2015, SŠ1 A 1
Dodao/la:
arhiva22. ožujka 2015. Neka su

i

različiti realni brojevi takvi da je
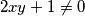
i neka su
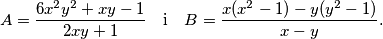
Odredi koji je broj veći,

ili

.
%V0
Neka su $x$ i $y$ različiti realni brojevi takvi da je $2xy + 1 \neq 0$ i neka su $$
A = \frac{6 x^2 y^2 + x y - 1}{2xy + 1}
\quad \text{i} \quad
B = \frac{x(x^2 - 1) - y(y^2 - 1)}{x - y} \text{.}
$$ Odredi koji je broj veći, $A$ ili $B$.
Izvor: Županijsko natjecanje iz matematike 2015