Za dani prirodni broj

neka je
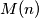
najveći prirodni broj za koji je moguće konstruirati niz prirodnih brojeva
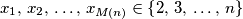
tako da vrijedi:
Za svaka dva različita broja 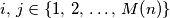 brojevi
brojevi 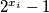
i
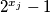 su relativno prosti.
su relativno prosti.Ako je
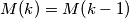
za neki prirodni broj

, dokaži da je

složen.
%V0
Za dani prirodni broj $n$ neka je $M\!\left(n\right)$ najveći prirodni broj za koji je moguće konstruirati niz prirodnih brojeva $x_1,\,x_2,\,\ldots,\,x_{M\!\left(n\right)} \in \left\{ 2,\,3,\,\ldots,\,n\right\}$ tako da vrijedi:
[i]Za svaka dva različita broja[/i] $i,\,j \in \left\{1,\,2,\,\ldots,\,M\!\left(n\right) \right\}$ [i]brojevi[/i] $2^{x_i}-1$ i $2^{x_j}-1$ [i]su relativno prosti.[/i]
Ako je $M\!\left(k\right) = M\!\left(k-1\right)$ za neki prirodni broj $k>1$, dokaži da je $k$ složen.