Županijsko natjecanje iz matematike 2016, SŠ3 A 5
Dodao/la:
arhiva1. svibnja 2017. Promatramo sve pravokutne ploče čija je polja moguće obojati tako da u svakom retku bude točno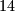 
plavih polja, u svakom stupcu točno 
crvenih polja i da na cijeloj ploči budu točno 
polja koja nisu ni crvena ni plava.
Odredi dimenzije takve ploče koja ima najmanji ukupan broj polja.
Promatramo sve pravokutne ploče čija je polja moguće obojati tako da u svakom retku bude točno $14$ plavih polja, u svakom stupcu točno $10$ crvenih polja i da na cijeloj ploči budu točno $3$ polja koja nisu ni crvena ni plava.
Odredi dimenzije takve ploče koja ima najmanji ukupan broj polja.
Izvor: Županijsko natjecanje iz matematike 2016
Školjka 
