Županijsko natjecanje 1994 SŠ1 4
Dodao/la:
arhiva1. travnja 2012. Za
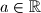
riješite sustav jednadžbi
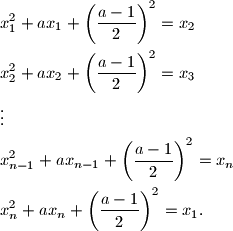
%V0
Za $a \in \mathbb{R}$ riješite sustav jednadžbi $$$\begin{align*}
&x_{1}^{2} + ax_{1} + \left( \frac{a-1}{2} \right)^{2} = x_{2}\\
&x_{2}^{2} + ax_{2} + \left( \frac{a-1}{2} \right)^{2} = x_{3}\\
&\vdots\\
&x_{n-1}^{2} + ax_{n-1} + \left( \frac{a-1}{2} \right)^{2} = x_{n}\\
&x_{n}^{2} + ax_{n} + \left( \frac{a-1}{2} \right)^{2} = x_{1}.
\end{align*}$$$
Izvor: Županijsko natjecanje iz matematike 1994