Državno natjecanje iz matematike 2016, SŠ2 A 4
Dodao/la:
arhiva1. svibnja 2017. Odredi sve trojke pozitivnih realnih brojeva 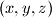 takve da vrijedi
takve da vrijedi 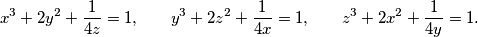
Odredi sve trojke pozitivnih realnih brojeva $(x, y, z)$ takve da vrijedi
$$
x^3 + 2y^2 + \frac{1}{4z} = 1 \text{,} \quad\quad
y^3 + 2z^2 + \frac{1}{4x} = 1 \text{,} \quad\quad
z^3 + 2x^2 + \frac{1}{4y} = 1 \text{.}
$$
Izvor: Državno natjecanje iz matematike 2016