Županijsko natjecanje 1996 SŠ1 1
Dodao/la:
arhiva1. travnja 2012. Neka je
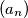
niz pozitivnih cijelih brojeva, takav da je

i
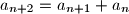
za
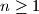
. Ako je
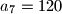
, koliko je
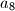
?
%V0
Neka je $(a_n)$ niz pozitivnih cijelih brojeva, takav da je $a_1<a_2$ i $a_{n+2}=a_{n+1}+a_n$ za $n \ge 1$. Ako je $a_7=120$, koliko je $a_8$?
Izvor: Županijsko natjecanje iz matematike 1996