Kružnice

i

s polumjerima
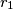
i
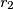
(
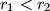
) dodiruju se iznutra u točki

. Neka je

jedna tangenta na

, koja ju dodiruje u točki

, i paralelna je zajedničkom promjeru danih kružnica. Neka su

i

sjecišta tangente

s

. Dokažite da je
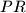
simetrala kuta
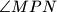
.
%V0
Kružnice $k_1$ i $k_2$ s polumjerima $r_1$ i $r_2$ ($r_1<r_2$) dodiruju se iznutra u točki $P$. Neka je $q$ jedna tangenta na $k_1$, koja ju dodiruje u točki $R$, i paralelna je zajedničkom promjeru danih kružnica. Neka su $M$ i $N$ sjecišta tangente $q$ s $k_2$. Dokažite da je $PR$ simetrala kuta $\angle MPN$.