MEMO 2015 pojedinačno problem 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Let 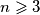 be an integer. An inner diagonal of a simple n-gon is a diagonal that is contained in the
be an integer. An inner diagonal of a simple n-gon is a diagonal that is contained in the  -gon. Denote by
-gon. Denote by 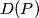 the number of all inner diagonals of a simple
the number of all inner diagonals of a simple  -gon
-gon  and by
and by 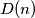 the least possible value of
the least possible value of 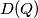 , where
, where  is a simple
is a simple  -gon. Prove that no two inner diagonals of
-gon. Prove that no two inner diagonals of  intersect (except possibly at a common endpoint) if and only if
intersect (except possibly at a common endpoint) if and only if 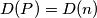 .
.
Remark: A simple  -gon is a non-self-intersecting polygon with
-gon is a non-self-intersecting polygon with  vertices. A polygon is not necessarily convex.
vertices. A polygon is not necessarily convex.
Izvor: Srednjoeuropska matematička olimpijada 2015, pojedinačno natjecanje, problem 2
 Školjka
Školjka 
