MEMO 2015 ekipno problem 6
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Let  be the incentre of triangle
be the incentre of triangle  with
with 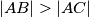 and let the line
and let the line 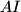 intersect the side
intersect the side  at
at  . Suppose that point
. Suppose that point  lies on the segment
lies on the segment  and satisfies
and satisfies 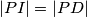 . Further, let
. Further, let 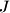 be the point obtained by reflecting
be the point obtained by reflecting  over the perpendicular bisector of
over the perpendicular bisector of  , and let
, and let  be the other intersection of the circumcircles of the triangles
be the other intersection of the circumcircles of the triangles  and
and 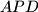 . Prove that
. Prove that 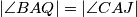 .
.
Izvor: Srednjoeuropska matematička olimpijada 2015, ekipno natjecanje, problem 6
 Školjka
Školjka 
