Školjka

A tract of land in the shape of an 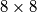$8 \times 8$ square, whose sides are oriented north–south and east–west, consists of 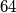$64$ smaller 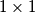$1 \times 1$ square plots. There can be at most one house on each of the individual plots. A house can only occupy a single 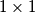$1 \times 1$ square plot. A house is said to be \emph{blocked from sunlight} if there are three houses on the plots immediately to its east, west and south. What is the maximum number of houses that can simultaneously exist, such that none of them is blocked from sunlight? Remark: By definition, houses on the east, west and south borders are never blocked from sunlight.