MEMO 2016 ekipno problem 5
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Let  be an acute-angled triangle with
be an acute-angled triangle with 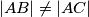 , and let
, and let  be its circumcentre. The line
be its circumcentre. The line 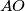 intersects the circumcircle
intersects the circumcircle  of
of  a second time in point
a second time in point  , and the line
, and the line  in point
in point  . The circumcircle of
. The circumcircle of 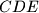 intersects the line
intersects the line  a second time in point
a second time in point  . The line
. The line 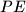 intersects the line
intersects the line  in point
in point  . The line through
. The line through  parallel to
parallel to 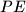 intersects the altitude of the triangle
intersects the altitude of the triangle  that passes through
that passes through  in point
in point  .
.
Prove that 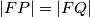 .
.
Izvor: Srednjoeuropska matematička olimpijada 2016, ekipno natjecanje, problem 5
 Školjka
Školjka 
