Školjka

• Natjecanja
• Shellfish
• Tečajevi
• MetaMath '24
• Izbornik
• Početna
• Arhiva zadataka
• Natjecanja
• Hrvatska
• Državna natjecanja
• Županijska natjecanja
• Srednja škola 4. razred
• Srednja škola 3. razred
• Srednja škola 2. razred
• Srednja škola 1. razred
• 2023
• 2022
• 2021
• 2020
• 2019
• 2018
• 2017
• 2016
• 2015
• 2014
• 2013
• 2012
• 2011
• 2010
• 2009
• 2008
• 2007
• 2006
• 2005
• 2004
• 2003
• 2002
• 2001
• 2000
• 1999
• 1998
• 1997
• 1996
• 1995
• 1994
• 1993
• 1992
• Osnovna škola 8. razred
• Općinska natjecanja
• Izborno natjecanje
• Hrvatska matematička olimpijada
• Olimpijade
• ELMO
• Europski matematički kup
• Skakavac
• Mathejeva mala (m)učionica
• MNM predavanja subotom
• Simulacije
• Kamp 2013
• RADDAR
• Predavanja
• Natjecanja
• Tečajevi
• 
  
• Registracija
• Prijava
• 
  
• Svi zadaci
• Rješenja
• Traži
• 
  
• 
  
• Pomoć
• O nama

Županijsko natjecanje 2005 SŠ1 3

Kvaliteta:

  Avg: 0,0

Težina:

  Avg: 3,0

Dodao/la: arhiva
1. travnja 2012.

2005 alg nejednakost ss1 zup

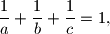
Ako su , , pozitivni realni brojevi takvi da je dokažite nejednakost

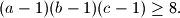
%V0 Ako su $a$, $b$, $c$ pozitivni realni brojevi takvi da je $$ \dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=1, $$ dokažite nejednakost $$ (a-1)(b-1)(c-1)\geq 8. $$