U krugu sa središtem u točki

, polumjera
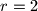
cm, povučena su dva polumjera
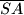
i
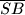
. Kut između njih je
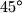
. Neka je

sjecište pravca

i okomice povučene na pravac
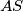
u točki

, a točka

je nožište visine trokuta
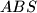
povučene iz vrha

. Izračunaj površinu trapeza
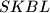
.
%V0
U krugu sa središtem u točki $S$, polumjera $r=2$ cm, povučena su dva polumjera $\overline{SA}$ i $\overline{SB}$. Kut između njih je $45^{\circ}$. Neka je $K$ sjecište pravca $AB$ i okomice povučene na pravac $AS$ u točki $S$, a točka $L$ je nožište visine trokuta $ABS$ povučene iz vrha $B$. Izračunaj površinu trapeza $SKBL$.