U šiljastokutnom trokutu

ortocentar raspolavlja visinu povučenu iz vrha
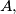
dok visinu povučenu iz vrha

dijeli u omjeru
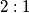
, tako da je ortocentar bliži nožištu visine nego vrhu. U kojem omjeru ortocentar dijeli visinu iz vrha

?
%V0
U šiljastokutnom trokutu $ABC$ ortocentar raspolavlja visinu povučenu iz vrha $A,$ dok visinu povučenu iz vrha $B$ dijeli u omjeru $2:1$, tako da je ortocentar bliži nožištu visine nego vrhu. U kojem omjeru ortocentar dijeli visinu iz vrha $C$?