Neka su

i

prirodni brojevi te
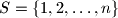
.

Odredi broj svih uređenih

-torki
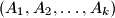
pri čemu su
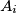
,
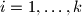
u parovima disjunktni podskupovi od

takvi da je
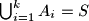
.

Odredi broj svih uređenih

-torki
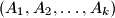
pri čemu su
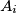
,
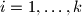
podskupovi (ne nužno disjunktni) od

takvi da je
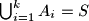
.
%V0
Neka su $n$ i $k$ prirodni brojevi te $S=\{1,2,\ldots,n\}$.
$a)$ Odredi broj svih uređenih $k$-torki $(A_1,A_2,\ldots,A_k)$ pri čemu su $A_i$, $i=1,\ldots,k$ u parovima disjunktni podskupovi od $S$ takvi da je \ $\bigcup_{i=1}^k A_i=S$.
$b)$ Odredi broj svih uređenih $k$-torki $(A_1,A_2,\ldots,A_k)$ pri čemu su $A_i$, $i=1,\ldots,k$ podskupovi (ne nužno disjunktni) od $S$ takvi da je \ $ \bigcup_{i=1}^k A_i=S$.