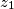
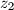
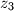
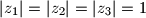
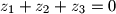
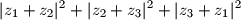
Neka su , i kompleksni brojevi takvi da je i . Dokažite da izraz poprima jednu te istu vrijednost za svaki izbor kompleksnih brojeva koji zadovoljavaju gornje uvjete.
%V0
Neka su $z_1$, $z_2$ i $z_3$ kompleksni brojevi takvi da je $|z_1|=|z_2|=|z_3|=1$ i $z_1+z_2+z_3=0$. Dokažite da izraz $$
|z_1+z_2|^2+|z_2+z_3|^2+|z_3+z_1|^2
$$ poprima jednu te istu vrijednost za svaki izbor kompleksnih brojeva koji zadovoljavaju gornje uvjete.
Školjka 
, 
i 
kompleksni brojevi takvi da je 
i 
. Dokažite da izraz 
poprima jednu te istu vrijednost za svaki izbor kompleksnih brojeva koji zadovoljavaju gornje uvjete.