MEMO 2019 pojedinačno zadatak 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka je 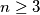 prirodni broj. Kažemo da je vrh
prirodni broj. Kažemo da je vrh 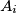
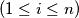 konveksnog mnogokuta
konveksnog mnogokuta 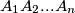 bohemijski ako se njegova centralnosimetrična slika u odnosu na polovište dužine
bohemijski ako se njegova centralnosimetrična slika u odnosu na polovište dužine 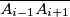 (uz
(uz  =
= 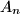 i
i 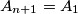 ) nalazi unutar ili na rubu mnogokuta
) nalazi unutar ili na rubu mnogokuta 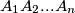 . Odredi najmanji mogući broj bohemijskih vrhova koje može imati konveksni
. Odredi najmanji mogući broj bohemijskih vrhova koje može imati konveksni  -terokut (ovisno o
-terokut (ovisno o  ).
).
(Konveksni mnogokut 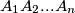 ima
ima  vrhova i sve unutarnje kutove manje od
vrhova i sve unutarnje kutove manje od 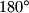 .)
.)
Izvor: Srednjoeuropska matematička olimpijada 2019, pojedinačno natjecanje, problem 2
 Školjka
Školjka 
