Europski matematički kup 2018. juniori 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka je  šiljastokutan trokut takav da je
šiljastokutan trokut takav da je 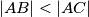 . Označimo s
. Označimo s  i
i  redom ortocentar trokuta
redom ortocentar trokuta  te polovište stranice
te polovište stranice  . Kružnica sa središtem u
. Kružnica sa središtem u  radijusa
radijusa 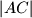 siječe opisanu kružnicu trokuta
siječe opisanu kružnicu trokuta  drugi put u točki
drugi put u točki  , a kružnica sa središtem u
, a kružnica sa središtem u  radijusa
radijusa 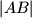 siječe dužinu
siječe dužinu 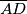 u točki
u točki  . Pravac kroz
. Pravac kroz  paralelan s
paralelan s  siječe
siječe  u točki
u točki  . Ako je
. Ako je  nožiste okomice iz
nožiste okomice iz  na
na 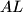 , dokaži da pravac
, dokaži da pravac  raspolavlja dužinu
raspolavlja dužinu 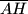 .
.
(Miroslav Marinov)
Izvor: Europski matematički kup 2018.
 Školjka
Školjka 
