U kompleksnoj ravnini promatrajte skup svih točaka

oblika
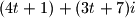
, gdje je

realan broj. Što je taj skup?
Odredite onaj broj iz tog skupa koji ima najmanju apsolutnu vrijednost.
%V0
U kompleksnoj ravnini promatrajte skup svih točaka $z$ oblika $(4t+1)+(3t+7)i$, gdje je $t$ realan broj. Što je taj skup?
Odredite onaj broj iz tog skupa koji ima najmanju apsolutnu vrijednost.