
Trokutu

upisana je kružnica koja redom dodiruje stranice

,

,

u točkama

,

,

. Dokažite da se pravci
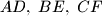
sijeku u istoj točki

.

Dokažite da nijedan od kutova
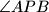
,
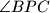
,
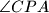
nije pravi.
%V0
$a)$ Trokutu $ABC$ upisana je kružnica koja redom dodiruje stranice $\overline{BC}$, $\overline{CA}$, $\overline{AB}$ u točkama $D$, $E$, $F$. Dokažite da se pravci $\;AD,\;BE,\;CF\;$ sijeku u istoj točki $P$.
$b)$ Dokažite da nijedan od kutova $\angle APB$, $\angle BPC$, $\angle CPA$ nije pravi.