Županijsko natjecanje 2001 SŠ2 2
Dodao/la:
arhiva1. travnja 2012. Ako su svakoj od jednadžbi
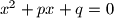
i
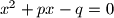
i gdje je
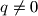
, oba rješenja cjelobrojna, dokažite da tada postoje prirodni brojevi

i

takvi da je
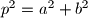
.
%V0
Ako su svakoj od jednadžbi $x^2+px+q=0$ i $x^2+px-q=0$ i gdje je $q\ne 0$, oba rješenja cjelobrojna, dokažite da tada postoje prirodni brojevi $a$ i $b$ takvi da je $p^2=a^2+b^2$.
Izvor: Županijsko natjecanje iz matematike 2001