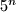
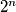
Neka su i prirodni brojevi. Dokažite da broj znamenaka u zapisu broja nije veći od , ako i samo ako broj znamenaka u zapisu broja nije manji od .
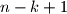
%V0
Neka su $n$ i $k$ prirodni brojevi. Dokažite da broj znamenaka u zapisu broja $5^n$ nije veći od $k$, ako i samo ako broj znamenaka u zapisu broja $2^n$ nije manji od $n-k+1$.
Školjka 
i 
prirodni brojevi. Dokažite da broj znamenaka u zapisu broja 
nije veći od 
nije manji od 
.