Odredi, ako postoji, realni parametar

takav da je maksimalna vrijednost funkcije
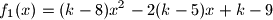
jednaka minimalnoj vrijednosti funkcije
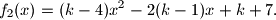
%V0
Odredi, ako postoji, realni parametar $k$ takav da je maksimalna vrijednost funkcije $$
f_1(x)=(k-8)x^2-2(k-5)x+k-9
$$ jednaka minimalnoj vrijednosti funkcije $$
f_2(x)=(k-4)x^2-2(k-1)x+k+7.
$$