Na promjeru  polukružnice sa središtem
polukružnice sa središtem  odabrana je točka
odabrana je točka  , različita od
, različita od  ,
,  i
i  . Iz točke
. Iz točke  povučena su dva polupravca pod jednakim kutovima na
povučena su dva polupravca pod jednakim kutovima na  koji sijeku polukružnicu u točkama
koji sijeku polukružnicu u točkama  i
i  (
( ). U točki
). U točki  povučena je okomica na polupravac
povučena je okomica na polupravac  koji siječe polukružnicu u točki
koji siječe polukružnicu u točki  . Dokažite da su, ako je
. Dokažite da su, ako je 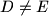 , pravci
, pravci 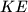 i
i  paralelni.
paralelni.
 polukružnice sa središtem
polukružnice sa središtem  odabrana je točka
odabrana je točka  , različita od
, različita od  ,
,  i
i  . Iz točke
. Iz točke  povučena su dva polupravca pod jednakim kutovima na
povučena su dva polupravca pod jednakim kutovima na  koji sijeku polukružnicu u točkama
koji sijeku polukružnicu u točkama  i
i  (
( ). U točki
). U točki  povučena je okomica na polupravac
povučena je okomica na polupravac  koji siječe polukružnicu u točki
koji siječe polukružnicu u točki  . Dokažite da su, ako je
. Dokažite da su, ako je 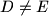 , pravci
, pravci 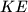 i
i  paralelni.
paralelni.  Školjka
Školjka