Na promjeru  polukružnice sa središtem
polukružnice sa središtem  odabrana je točka
odabrana je točka  , različita od
, različita od  ,
,  i
i  . Iz točke
. Iz točke  povučena su dva polupravca pod jednakim kutovima na
povučena su dva polupravca pod jednakim kutovima na  koji sijeku polukružnicu u točkama
koji sijeku polukružnicu u točkama  i
i  (
(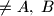 ). U točki
). U točki  povučena je okomica na polupravac
povučena je okomica na polupravac  koji siječe polukružnicu u točki
koji siječe polukružnicu u točki  . Dokažite da su, ako je
. Dokažite da su, ako je 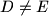 , pravci
, pravci 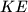 i
i  paralelni.
paralelni.
 polukružnice sa središtem
polukružnice sa središtem  odabrana je točka
odabrana je točka  , različita od
, različita od  ,
,  i
i  . Iz točke
. Iz točke  povučena su dva polupravca pod jednakim kutovima na
povučena su dva polupravca pod jednakim kutovima na  koji sijeku polukružnicu u točkama
koji sijeku polukružnicu u točkama  i
i  (
(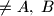 ). U točki
). U točki  povučena je okomica na polupravac
povučena je okomica na polupravac  koji siječe polukružnicu u točki
koji siječe polukružnicu u točki  . Dokažite da su, ako je
. Dokažite da su, ako je 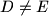 , pravci
, pravci 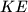 i
i  paralelni.
paralelni. Slični zadaci
Oko kružnice polumjera  položeno je šest kružnica polumjera
položeno je šest kružnica polumjera  , tako da svaka dodiruje izvana središnju kružnicu (polumjera
, tako da svaka dodiruje izvana središnju kružnicu (polumjera  ) i dvije susjedne kružnice polumjera
) i dvije susjedne kružnice polumjera  . Oko ovih kružnica položeno je još šest većih kružnica polumjera
. Oko ovih kružnica položeno je još šest većih kružnica polumjera  , od kojih svaka dodiruje izvana dvije kružnice polumjera
, od kojih svaka dodiruje izvana dvije kružnice polumjera  i dvije veće kružnice (polumjera
i dvije veće kružnice (polumjera  ). Izračunajte polumjere
). Izračunajte polumjere  i
i  .
.
 položeno je šest kružnica polumjera
položeno je šest kružnica polumjera  , tako da svaka dodiruje izvana središnju kružnicu (polumjera
, tako da svaka dodiruje izvana središnju kružnicu (polumjera  ) i dvije susjedne kružnice polumjera
) i dvije susjedne kružnice polumjera  . Oko ovih kružnica položeno je još šest većih kružnica polumjera
. Oko ovih kružnica položeno je još šest većih kružnica polumjera  , od kojih svaka dodiruje izvana dvije kružnice polumjera
, od kojih svaka dodiruje izvana dvije kružnice polumjera  i dvije veće kružnice (polumjera
i dvije veće kružnice (polumjera  ). Izračunajte polumjere
). Izračunajte polumjere  i
i  .
.  Školjka
Školjka 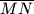 kružnice. Neka je
kružnice. Neka je  tangenta te kružnice u točki
tangenta te kružnice u točki  te neka su točke
te neka su točke 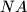 i
i 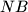 s pravcem
s pravcem 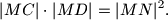
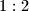 . U veći od ta dva dijela upisan je kvadrat čija jedna stranica leži na toj tetivi. Odredi duljinu stranice tog kvadrata.
. U veći od ta dva dijela upisan je kvadrat čija jedna stranica leži na toj tetivi. Odredi duljinu stranice tog kvadrata. 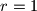 postavljeno je unutar kružnice polumjera
postavljeno je unutar kružnice polumjera  i
i  s polumjerima
s polumjerima 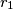 i
i 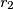 (
(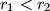 ) dodiruju se iznutra u točki
) dodiruju se iznutra u točki  . Neka je
. Neka je  jedna tangenta na
jedna tangenta na  sjecišta tangente
sjecišta tangente 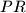 simetrala kuta
simetrala kuta 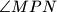 .
.