Dvije kružnice jednakog polumjera
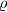
upisane su u trokut

tako da se međusobno dodiruju, te jedna od njih dodiruje stranice

i

, a druga stranice

i

. Dokaži da vrijedi
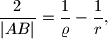
gdje je

polumjer upisane kružnice trokuta

.
%V0
Dvije kružnice jednakog polumjera $\varrho $ upisane su u trokut $ABC$ tako da se međusobno dodiruju, te jedna od njih dodiruje stranice $\overline{AB}$ i $\overline{AC}$, a druga stranice $\overline{AB}$ i $\overline{BC}$. Dokaži da vrijedi $$
\dfrac{2}{|AB|}=\dfrac{1}{\varrho }-\dfrac{1}{r},
$$ gdje je $r$ polumjer upisane kružnice trokuta $ABC$.