Slični zadaci
Oko kružnice polumjera  položeno je šest kružnica polumjera
položeno je šest kružnica polumjera  , tako da svaka dodiruje izvana središnju kružnicu (polumjera
, tako da svaka dodiruje izvana središnju kružnicu (polumjera  ) i dvije susjedne kružnice polumjera
) i dvije susjedne kružnice polumjera  . Oko ovih kružnica položeno je još šest većih kružnica polumjera
. Oko ovih kružnica položeno je još šest većih kružnica polumjera  , od kojih svaka dodiruje izvana dvije kružnice polumjera
, od kojih svaka dodiruje izvana dvije kružnice polumjera  i dvije veće kružnice (polumjera
i dvije veće kružnice (polumjera  ). Izračunajte polumjere
). Izračunajte polumjere  i
i  .
.
 položeno je šest kružnica polumjera
položeno je šest kružnica polumjera  , tako da svaka dodiruje izvana središnju kružnicu (polumjera
, tako da svaka dodiruje izvana središnju kružnicu (polumjera  ) i dvije susjedne kružnice polumjera
) i dvije susjedne kružnice polumjera  . Oko ovih kružnica položeno je još šest većih kružnica polumjera
. Oko ovih kružnica položeno je još šest većih kružnica polumjera  , od kojih svaka dodiruje izvana dvije kružnice polumjera
, od kojih svaka dodiruje izvana dvije kružnice polumjera  i dvije veće kružnice (polumjera
i dvije veće kružnice (polumjera  ). Izračunajte polumjere
). Izračunajte polumjere  i
i  .
.  Školjka
Školjka 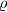 upisane su u trokut
upisane su u trokut  tako da se međusobno dodiruju, te jedna od njih dodiruje stranice
tako da se međusobno dodiruju, te jedna od njih dodiruje stranice  i
i  , a druga stranice
, a druga stranice  . Dokaži da vrijedi
. Dokaži da vrijedi 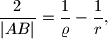 gdje je
gdje je 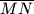 kružnice. Neka je
kružnice. Neka je  tangenta te kružnice u točki
tangenta te kružnice u točki  te neka su točke
te neka su točke  i
i  redom sjecišta pravaca
redom sjecišta pravaca 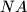 i
i 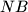 s pravcem
s pravcem 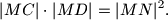
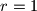 postavljeno je unutar kružnice polumjera
postavljeno je unutar kružnice polumjera 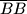 i
i 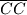 . Kroz ortocentar
. Kroz ortocentar  je povučen pravac koji siječe stranice trokuta
je povučen pravac koji siječe stranice trokuta  . Neka je
. Neka je 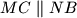 .
. 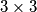 treba upisati prirodne brojeve, tako da u svakom retku i svakom stupcu produkt upisanih brojeva bude
treba upisati prirodne brojeve, tako da u svakom retku i svakom stupcu produkt upisanih brojeva bude 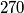 . Na koliko je načina to moguće napraviti?
. Na koliko je načina to moguće napraviti?